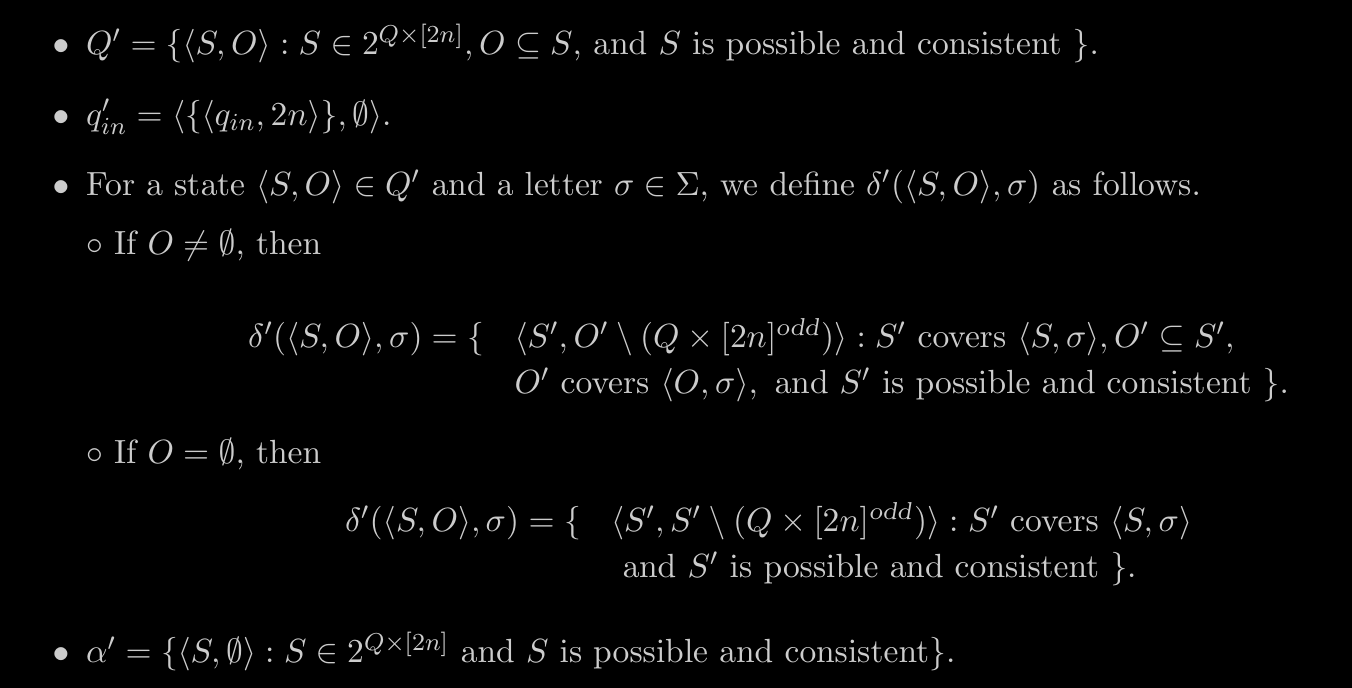# Weak Alternating # Automata are # not that weak Jessica, Shubh and and Sreevani

April, 2024

---

Alternating Automata

An alternating automata is defined by the following tuple $⟨Q,\Sigma ,q_{in},\delta ,\alpha ⟩$ where $\delta :Q\times \Sigma \to {\mathcal{B}}^{+}(Q)$

Weak Alternating Automata

It is an Alternating Automata where

• $Q={⨆}_{i\in [k]}{Q}_i$ such that $Q_i\subseteq \alpha$ or $Q_i\cap \alpha =\varnothing$
• There is a partial order $\le$ on the partition such that any transition goes to a state in partition that is less than or equal to the current one.

note: State the true-false thingy

---

Runs in Alternating Automata

Runs in alternating automata can be represented as trees in the following way $⟨T_r,r⟩⟨⟩⟨⟩$ where $r$ is a labelling function from nodes of $T_r$ to $Q$

note: Nodes of T_r representation

—

Memoryless Runs

Similar Nodes

Two nodes are called similar if

• They have the same depth
• They are labelled by the same state

Memoryless runs

A run is called memoryless if subtrees of similar any pair of nodes are identical

lemma

Any accepting word has a accepting memoryless run on an Alternating Co-Buchi Automata.

note: The Lemma is for Parity Automata(games i think lol) Alternating Co-Buchi is a special case

---

DAG representation

Quotienting similar nodes together to get a Directed Acyclic Graph from a tree $G_r$.

• Endangered: Only finitely many states are reachable
• Safe: No $\alpha$ state is reachable

note: DRAWWWWWW mention progress measures rank is like ease of acceptance proof

—

Rank

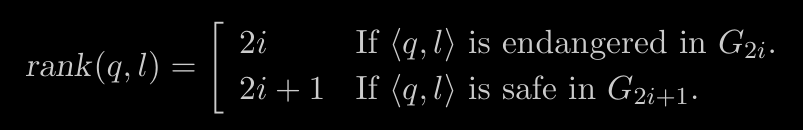
Lemma

For every $i>0$, there exists $d_i$ such that forall $d\ge d_i$, there are at most $n-i$ vertices at depth $d$

note: mention odd for safe and even for endangered Induction,

• If finite then trivial
• Otherwise G_i+1 is infinte and we can find a safe state

Lemma : G2n is finite hence finite rank

—

Lemma

For any two states $s_1=⟨q_i,i⟩$ and $s_2=⟨q_j,j⟩$, if $s_2$ is reachable from $s_1$ then rank of $s_2$ is less than the rank of $s_1$

Final Lemma

In an infinite path on $G_r$ there exists $⟨q,l⟩$ such that every node after it in the run has the same rank as itself which must be even.

note: if $s_1$ is removed, its remaining descendants
Induction : find fixpoint. And it cannot be even because infinte chain

---

Alternating Co-Buchi to Weak Alternating Automata

Theorem

For every Alternating Co-Buchi Automata $A_C$, there exists a Weak Alternating Automata $W$ such that $\mathcal{L}(W)={\mathcal{A}}_C$ and there is a quadratic blowup in number of states.

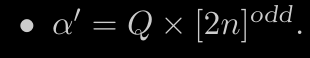
note: Weak..duh L(W)⇐ L(A_c) ⇒ (Tr, r) in W and (Tr, r’) in A_c such that r(x) = q_i, n and r’(x) = q_i (projection). L(A_c)⇐ L(W) ⇒ (Tr, r) in A_c, just get the ranks from constructions

Release Function replacing an atom q by disjuction of (q,i)

—

Alternating Buchi to Weak Alternating Automata

• Complement Buchi by taking a dual and produce Alternating Co-Buchi
• Convert CoBuchi to WAA
• Complement WAA (dual of edges and complement of good states)

—

Improving Construction

Required Rank

We say that $j\in [n]$ is required for $w$ iff there exists $w\in \mathcal{L}(W)$ such that for every memoryless run $⟨T_r,r⟩$ of $W$ on $w,G_{2j+1}\ne \varnothing$

Minimal rank

Minimal rank is the max required rank

—

Complexity of Finding the Minimal Rank

Theorem

Let $A_C$ be an alternating co-Buchi Automaton. The problem of finding minimal rank is $\text{PSPACE-Complete}$ .

---

Complementing Buchi Automata

Theorem

Let $A_B$ be an alternating Buchi Automata. There is a NBA $N$ with exponentially many states such that $\mathcal{L}(N)=\mathcal{L}(A_B)$.

The Construction is as follows

• Given $A_B=⟨\Sigma ,Q,q_{in}\delta ,\alpha ⟩$ we construct
• $N=⟨\Sigma ,2^Q\times 2^Q,(\{q_{in}\},\varnothing ),{\delta }^{\prime },2^Q\times \{\varnothing \}⟩$

—

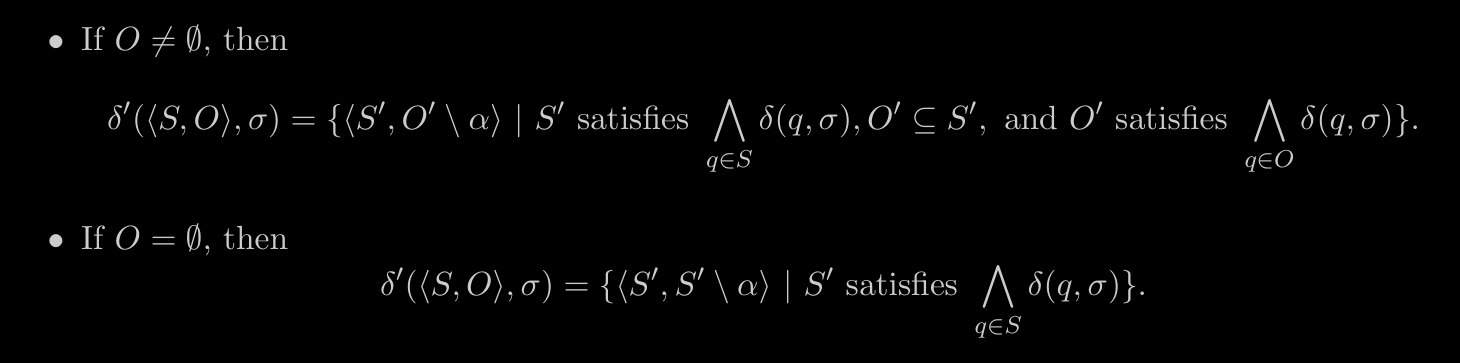
The Actual Thing

Given the above construction

1. we build from $N$ its dual co-Buchi universal automaton $A_C$. The automaton $A_C$ satisfies $\mathcal{L}(A_C)={\Sigma }^{\omega }\setminus \mathcal{L}(N)$.
2. construct from $A_C$ its equivalent weak alternating automaton $W$. The automaton $W$ satisfies $\mathcal{L}(W)={\Sigma }^{\omega }\setminus \mathcal{L}(N)$
3. construct from $W$ its equivalent nondeterministic Buchi automaton $N_C$. The automaton $N_C$ satisfies $\mathcal{L}(N_c)={\Sigma }^{\omega }\setminus \mathcal{L}(N)$.

note: draw this on the board

—

Optimizing Construction

We shall restrict the set of states to set of size $2^{O(n\log n)}$ by using the following definition by using the structure of the weak alternating automata.

Consistent

We say that a subset $S$ is consistent if $(q,i)\in S$ and $(q,j)\in S$ implies $i=j$

—

Final Construction