## Almost Certain Model Chekcing Shubh Sharma

NOVEMBER, 2023

---

Outline

1. Introduction
2. Linear Temporal Logic
3. Timed Automata
4. Probabilistic Semantics
5. Topological Semantics
6. Correspondence of the two Semantics
7. Model Checking Hardness

---

Introduction

Timed Automata are really nice (=

They let us describe systems with real-time constraints but still satisfy a lot of nice properties like reachability, safety properties, etc ,etc.

But

---

Timed Automata are too nice )=

Like most mathematical objects, they several assumptions made about them like infinite precision, instantaneous events which are unrealistic

So we discuss two semantics for Linear Time Logic using timed automata that let us model check ignoring cases that are too unlikely/extreme a topological and a probabilistic one.

---

Linear Temporal Logic

Temporal Logics introduce operators that describe how the world changes without explicitly referring to time. This helps us guarantee properties like

• Safety: Anything bad will not happen
• Liveness: Something good will happen
• Fairness: Evolution of subsystems

— Linear Temporal Logic introduces operators with the assumption that there is one execution path in time. That is, we sort of know what how the evolution of the system will be.

---

Syntax

We have a set of Atomic proposition $\mathcal{P}$ and the formulae satisfy the following grammar.

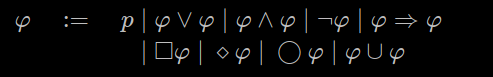
— where the 4 temporal operators are

• $◯f$ : $f$ is true in the next state
• $\square f$ : $f$ will be true in all future states
• $\diamond f$ : $f$ is true in some future state
• $f\cup g$ : $g$ will be true in some state in the future, $f$ is true in each state until then

And $p\in \mathcal{P}$

---

Semantics

The idea is to model a world, that evolves with time, and at every evolution(discrete) some statements are true. We do logic at a particular time in the world and we need to make relations between statements across time.

To give the semantics, we define a satisfactory relation $\models$ of the type $(\mathbb{N}\to 2^{\mathcal{P}})\times \mathbb{N}\times LTL$.

We define the boolean operators in the usual manner, for the rest of the operators

—

Propositions

$$(\sigma ,j)\models p\text{iff}p\in \sigma (j)$$

—

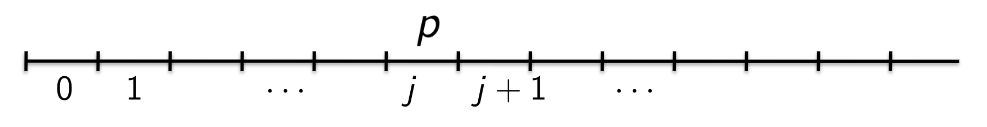
Next

$$(\sigma ,j)\models ◯p\text{iff}(\sigma ,j+1)\models p$$

—

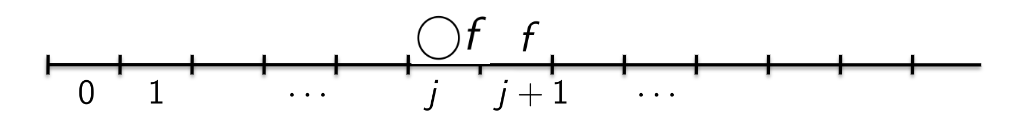
Henceforth

$$(\sigma ,j)\models \square p\text{iff}\forall k\cdot (k\ge j\Rightarrow (\sigma ,k)\models p)$$

—

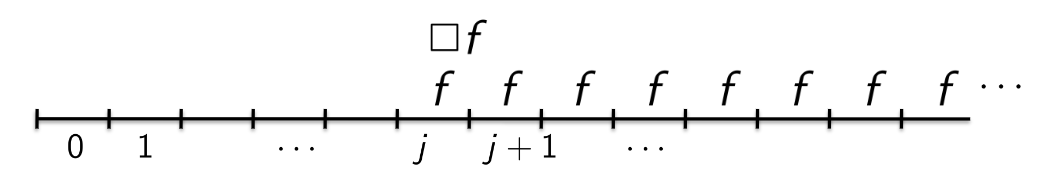
Until

$$(\sigma ,j)\models f\cup g\text{iff}\exists k\cdot (A\wedge B)$$

where

• $A=k\ge j\Rightarrow (\sigma ,k)\models g$
  • $g$ will happen
• $B=\forall i\cdot (j\le i<k\Rightarrow (\sigma ,i)\models f)$
  • $f$ keeps happening $g$

---

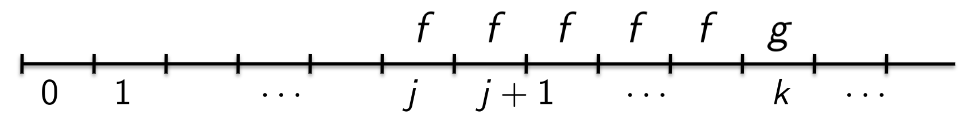
Timed Automata

Now we can formally define Timed Automata

We define a timed automaton $\mathcal{A}$ as the tuple

$$\mathcal{A}=⟨L,X,E,\mathcal{I},\mathcal{L}⟩$$

—

$$\mathcal{A}=⟨L,X,E,\mathcal{I},\mathcal{L}⟩$$

• $L$ : Location / States
• $X$ : Clocks
• $E\subseteq L\times \mathcal{G}(X)\times 2^X\times L$ : Edges
  • State + Guard + Resets → State
• $\mathcal{I}:L\to \mathcal{G}(X)$ : Invariant
• $\mathcal{L}:L\to 2^{\text{AP}}$
  • $\text{AP}$ is a finite set of atomic propositions
  • Assignment of a logical proposition to each location.

— Semantics of a Timed Automata $\mathcal{A}$ is given by a labelled Transition system $T_{\mathcal{A}}$

$$T_{\mathcal{A}}=⟨S,E\bigsqcup {\mathbb{R}}_{+},\to ⟩$$

• $S$ is a set of states/symbolic states $\{s=(l,\nu )\in L\times {\mathbb{R}}_{+}^X:\nu \models \mathcal{I}(l)\}$
  • The clock valuations need to respect the state invariant
• We gave 2 kinds of transtions
  • Discrete transitions
  • Delay transitions
  • And in both cases state invariants should be respected at all times

— $\mathcal{A}$ is said to be non-blocking if $I(s)\ne \varnothing$ for all $s$.

We define a symbolic path as a state, followed by a sequence of edges, such that the delay transitions follow a certain constraint

Example

---

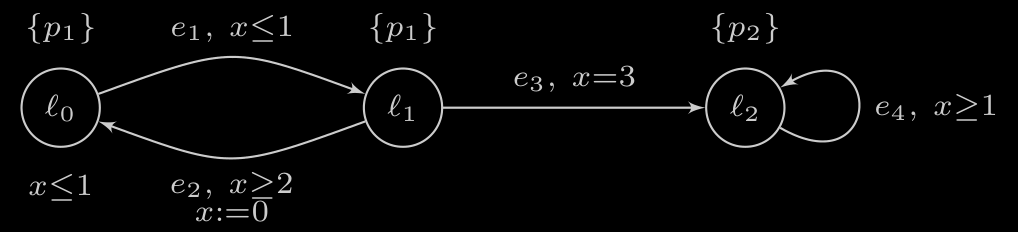
Region Automata

Here, we will modify the region automaton to be a timed automaton. The goal is to use this, as a more well behaved and easy to work version of the original automaton, that satisfies some strong properties which will be discussed later.

— Let ${\mathcal{R}}_{\mathcal{A}}$ be the set of regions in $\mathcal{A}$, then the region automata ${\text{R}}_{\mathcal{A}}$ is $⟨Q,X,T,\kappa ,\lambda ⟩$ such that

• $Q=L\times {\mathcal{R}}_{\mathcal{A}}$
• $\kappa ((l,\tau ))=\mathcal{I}(l)$
• $\lambda ((l,r))=\mathcal{L}(l)$
• $X$ is the same set of clocks
• $T\subseteq Q\times \text{cell}(R_{\mathcal{A}})\times E\times 2^X\times Q$, so $(l,r)\stackrel{\text{cell}(r^{\prime \prime }),e,Y}{\to }(l^{\prime },r^{\prime })$ exists if

we can recover the usual region automata by getting rid of time constraints and clocks.

—

Important Property

Path correspondence: every finite path $\pi ((l,\nu ),e_1\dots e_n)$ in $\mathcal{A}$ has a finite set of corresponding paths $\pi (((l,[\nu ]),\nu ),f_1\dots f_n)$ in ${\text{R}}_{\mathcal{A}}$. Each path in the set represents the choice of regions and delays taken while traversing the above path in $\mathcal{A}$

Also, if $A$ is non-blocking, so is ${\text{R}}_{\mathcal{A}}$

---

Probabilistic Semantics

We will now build some machinery to give probabilistic semantics for LTL formulae

We define a probability measure for $I(s)$ and a probability measure on the set of enabled transitions. Extending this will give a probability measure on runs.

---

Probability measure on $I(s)$ and edges

Our probability measure ${\pi }_s$ need to satisfy the following propeties

• ${\pi }_s(I(s))=1$
• given the Lebesgue measure $\lambda$ if $I(s)$ is not finite, ${\mu }_s$ should be equivalent to $\lambda$, otherwise it is uniform over the points
• Given any $s$, we also define a probability measure $p_s$ on the set of enabled edges

—

Example

• Uniform Distribution over $I(s)$ if it is finite.
• Lebesgue Measure normalised to have a probability measure if $I(s)$ is a finite set of bounded intervals.
• Exponential distribution if $I(s)$ contains an unbounded interval.

The exact measure does note matter as the property we desire are qualitative.

---

Probability measure on Finite Paths

Given a finite path $\pi (s,e:es)$ , we can define the probability measure on the path as

$${\mathbb{P}}_{\mathcal{A}}(\pi (s,e:es))=\frac{1}{2}{\int }_{t\in I(s,e_1)}{p}_{s+t}(e){\mathbb{P}}_{\mathcal{A}}(\pi (s^{\prime },es))d{\mu }_s(t)$$

This gives a probability distribution on $\text{Runs}(\mathcal{A},s)$

Sanity Check!

• Ignore the $\frac{1}{2}$ for now
• Its the probability of that $e_1$ is picked and the rest of the path can be traversed, given that $t$ time has elapsed.
• Integrate that over all $t\in I(s,e_1)$
• For this situation, summing the probabilities of all paths of length $n$ is $1$
• $\frac{1}{2}$ is just the normalisation factor such that now the total probability of a path of any length is $1$

—

Example

---

Similar measures on $\mathcal{A}$ and ${\text{R}}_{\mathcal{A}}$

We assume that for every state ${\mu }_s^{\mathcal{A}}={\mu }_{\iota (s)}^{{\text{R}}_{\mathcal{A}}}$ this is possible because we have that $I(s)=I(\iota (s))$ If $p^{\mathcal{A}}$ is distributed over edges in $\mathcal{A}$, we assume that for every state $s$ in $\mathcal{A}$ and $t\in {\mathbb{R}}_{+}$ $p_{s+t}^{\mathcal{A}}=p_{\iota (s)+t}^{{\text{R}}_{\mathcal{A}}}$

This also gives us that probability of a path in $\mathcal{A}$ is the same as probability of its projection in ${\text{R}}_{\mathcal{A}}$.

---

Probabilistic Semantics for LTL

We consider runs of a timed automaton as sequences of worlds over which we give semantics for our LTL formulae.

Here we see $\mathcal{L}$ begin used for the very first time. This is like the function which assigns worlds atomic proposition.

---

Probability on LTL Formulae

Since satisfiability only depends on states, either all, or none of the runs in a path satisfy the formula. Hence we give probability to an LTL formula $\phi$ from $s$ as

Which is the total probability of all paths that satisfy $\phi$.

---

Satisfying LTL formulae

We say that $\mathcal{A}$ almost surely satisfies $\phi$ from $s_0$ wrt ${\mathbb{P}}_{\mathcal{A}}$ and write $\mathcal{A},s_0\mid {\approx }_{\mathbb{P}}\phi$ iff ${\mathbb{P}}_{\mathcal{A}}(s_0,\phi )=1$.

And because of the earlier claim we have.

---