202311031611

Tags : Timed Automata

Alternating Timed Automata

---

Definition

An Alternating Timed Automaton is a tuple $⟨Q,q_0,\Sigma ,X,T,F⟩$ where

• $Q$ is a set of states
• $q_0\in Q$ is the starting state
• $X$ is a set of clock
• $\Sigma$ is the alphabet
• $F$ is the set of final states.
• $T:Q\times \Sigma \times \Phi (X)\to \mathcal{P}(Q\times \mathcal{P}(X))$ is the set of transitions or
• $T:Q\times \Sigma \times \Phi (X)\to {\mathcal{B}}^{+}(Q\times \mathcal{P}(X))$

Intuitively, given a state and a transition that can satisfied you return a set of states and resets for each of the states, such that from each of those states, there should be an accepting run. Or it goes to a boolean formula of states that represents both disjunctions and conjunctions of runs.

---

Accepting runs

Given a transition in an Alternating Timed Automaton

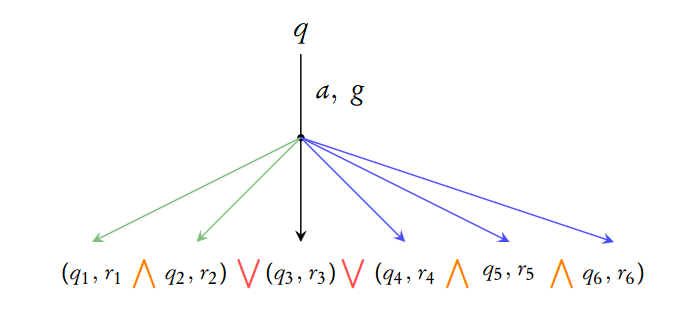
There is an accepting run from $q$ if

• There is an accepting run from each of$q_1$ and $q_2$ after the transition. or
• There is an accepting run from $q_3$ after the transition, or
• There is an accepting run from each of $q_1$, $q_2$ and $q_3$ after the transition.

Acceptance Game

There is a game corresponding to the acceptance of a given word ina timed automata that can be played between $2$ players such that if one the players has a winning strategy then the word is accepted.

Construction and Gameplay

Given a timed word $w\in (\Sigma ,T{)}^{\ast }$ we construct a graph such that we construct a tree for a timed automata, and we start at the starting state as the root. Then for each transition to an element of $b\in B^{+}(Q\times \mathcal{P}(X))$
If $b$ if of the from

• $b_1\wedge b_2\dots b_n$ then Player 1 chooses a sub-formula
• $b_1\vee b_2\dots b_n$ then Player 2 chooses a sub-formula After we reach an atomic formula $p$ we pick the corresponding transition in the graph keep repeating this until the word is fully red

Winning Scenarios

We say that Player 2 wins, if the final state that the game ends on is a final state, otherwise Player 1 wins

We say that a word is accepted iff Player 2 has a winning strategy

Example

Running the alternating timed automaton given in the Example section, we can construct the following graph for its runs on the word $\{aaa,(0.3,0.8,1.5)\}$

Transclude of Alternating-Timed-Automata-Game-Example.excalidraw

Here, Player 1 has a choice to make on the first step, but whatever they do, they eventually reach a final state. Hence Player 2 will always win. Hence the word will be accepted.

The correctness of the game is trivial.

---

Closure Properties

Alternating Timed Automata are closed under

• Union and Intersection (use the new transition to directly get a new construction)
• Complementation (Replace all the accepting and non accepting states, and switch all $\wedge$ and $\vee$ in the transition)

This shows that Alternating Timed Automata are strictly more powerful than timed automata as the languages accepted by these are closed under complementation.

---

Example

Transclude of Timed-Automata-Example.excalidraw

---

References

Expressability of One-Clock Alternating Timed Automata Alternating Finite Automaton