202501162201

Tags : Weighted Automata and Transducers

Algorithm for Finding the Weight of a Word

---

This is the WA variant of checking for acceptance of a word.

---

Lazy Power Set Idea

This algorithm is similar to that of the lazy power set construction for checking an acceptance of a word in a Non-Deterministic Finite State Automata.

The Idea is to start with a set of start states, along with the weights, and then on each step apply the transition to all states to obtain the new set of weights. If two different states go to the same one, then add their weights.

Algorithm:

• Let $S$ be a set of start states along with their start weights.
• For $a$ in $w$:
  • For each $s$ in $S$ and each transition $(s,s^{\prime },w)$ in the set of transtions, add $s^{\prime }$ to $S^{\prime }$ with the weight $w$ multiplied to the weight with $s^{\prime }$.
  • For $(s^{\prime },w)$ and $(s^{\prime },w^{\prime })$ in $S^{\prime }$, replace it with $(s^{\prime },w+w^{\prime })$ until there are no repeated.
    • This step is what keeps the time complexity good and is only possible because of
  • Replace $S$ with $S^{\prime }$
• Multiply the final state weights to all every state in $S$ and add them together.

---

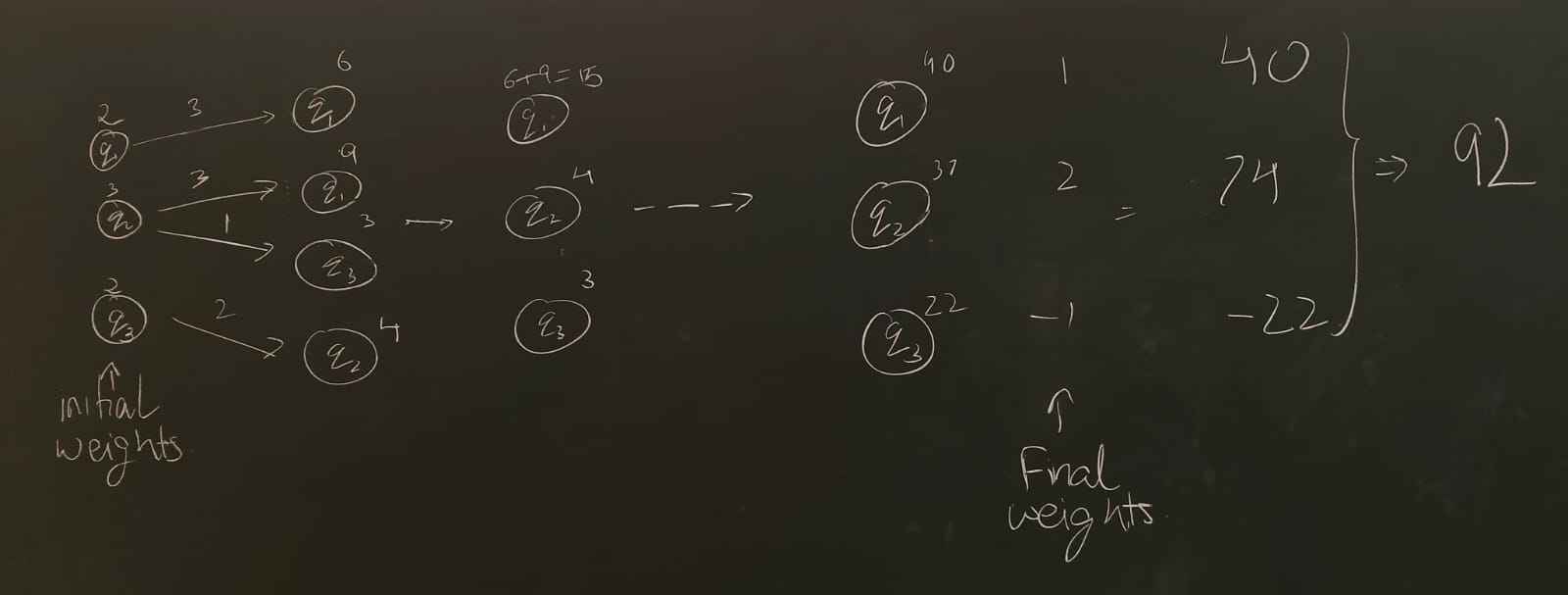
Matrix Implementation

After $k$ alphabets are read, one can think of the set of states and weights associated with them as a $|Q|$ sized vector.

If one represents the state of the weighted automata in that manner, then transition by reading a letter ${\mu }_a$ can be written as

$$\left(\begin{array}{cccc}{w}_{1,1}& w_{1,2}& \cdots & w_{1,|Q|}\\ w_{2,1}& w_{2,2}& \cdots & w_{2,|Q|}\\ ⋮& ⋮& \ddots & ⋮\\ w_{|Q|,1}& w_{|Q|,2}& \cdots & w_{|Q|,|Q|}\end{array}\right)$$

Where $w_{x,y}=\mu (x,y)$.

Algorithm:

• Write $I$ as a $1\times |Q|$ matrix, $F$ as a $|Q|\times 1$ matrix and for each $a$ construct $m_a$ from ${\mu }_i$.
• Let $V=I$
• For $w_i\in w_1{w}_2\dots w_n=w$:
  • $V=V\cdot m_{w_i}$
• $V=V\cdot F$
• return $V$

Here $V$ starts as a $1\times Q$ matrix and is multiplied by a sequence of $Q\times Q$ matrices, so the order remains the same.

In the final step, $V$ is multiplies by $F$ giving a $1\times 1$ matrix formed by multiplying final values for each state and adding them up.

---

References