# Complexity of MSO # On words Shubh and Sreevani

March, 2024

---

Theorem

Assume $P\ne NP$. Let $f$ be an elementary function and $p$ a polynomial, then there is no model checking algorithm for monadic-second order logic on the class of words whose running time is bounded by $f(k)\cdot p(n)$

note:

• PSPACE-Complete but words >>> formula irl.
• Separate it out by considering FPT

—

FPT

A parameterized problem is called **fixed parameter tractable** if it can be solved in the time $$ \begin{align} &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;f(k)\cdot p_k(n) \\ \text{where}\; & f \text{ is an arbitrary computable function} \\ & \quad\quad p_{k} \text{ is some polynomial.} \end{align} $$

note:

• Problem is in FPT
  • Buchi Theorem
    • build automata in time $f$
    • word check time linear
• Still infeasible, so we want to try to bound $f$

—

Elementary Functions

A function $f$ is elementary if $\exists m,f(x)\le 2^{2^{{.}^{{.}^{2^x}}}}$ where the power tower has height $m$.

note:

• We show that if it not possible by contradiction
  • give an efficient encoding for CNF + tiny formula
  • fast model checking algo $⟹$ Sat can be solved in $P$

---

Efficient Encoding for $\mathbb{N}$

note:

• CNF assignment
  • variables indexed by nats
  • find the variable of the CNF in the assignment
  • tiny formula to compare nats

—

$$\begin{array}{rl}{\mu }_1(0)& =⟨1⟩⟨/1⟩\\ {\mu }_1(n)& =⟨1⟩\text{bin}(n-1)⟨/1⟩\end{array}$$

And we have the following formula that checks if two encodings of natural numbers starting at positions $x$ and $y$ are the same.

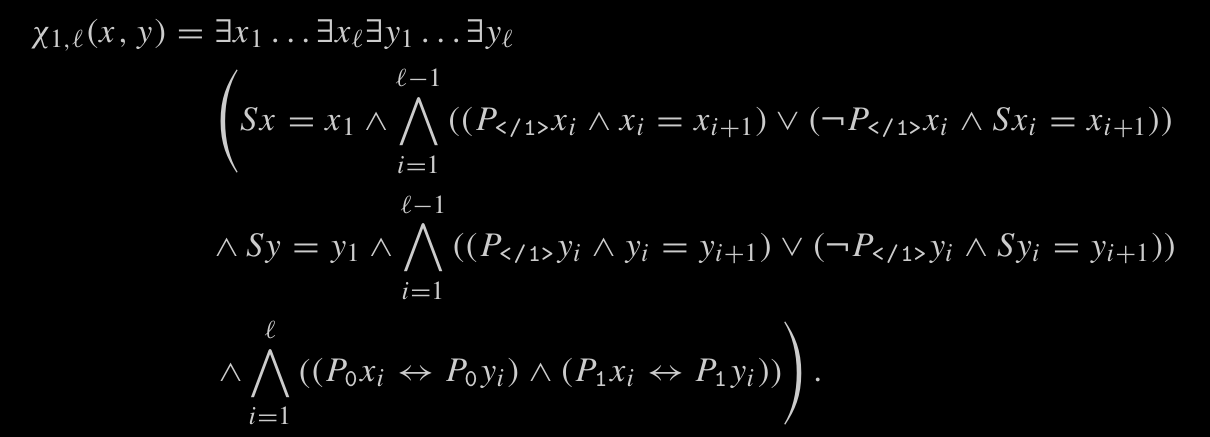
note:

• write formula and tell that its linear
• tell that it can check numbers of size up to $2^n$
• Motivation for general case
  • write by had $m{u}_2$
  • And show how easy it is to write a formula for $2^{2^n}$

—

$$\begin{array}{rl}{\mu }_h(n)=⟨h⟩& \\ & {\mu }_{h-1}(0)\text{ bin}(n-1)[0]\\ & ⋮\\ & {\mu }_{h-1}(d)\text{ bin}(n-1)[d]\\ ⟨/h⟩& \end{array}$$

And two numbers encoded by ${\mu }_h$ starting at positions $x$ and $y$ can be equated by the following formula.

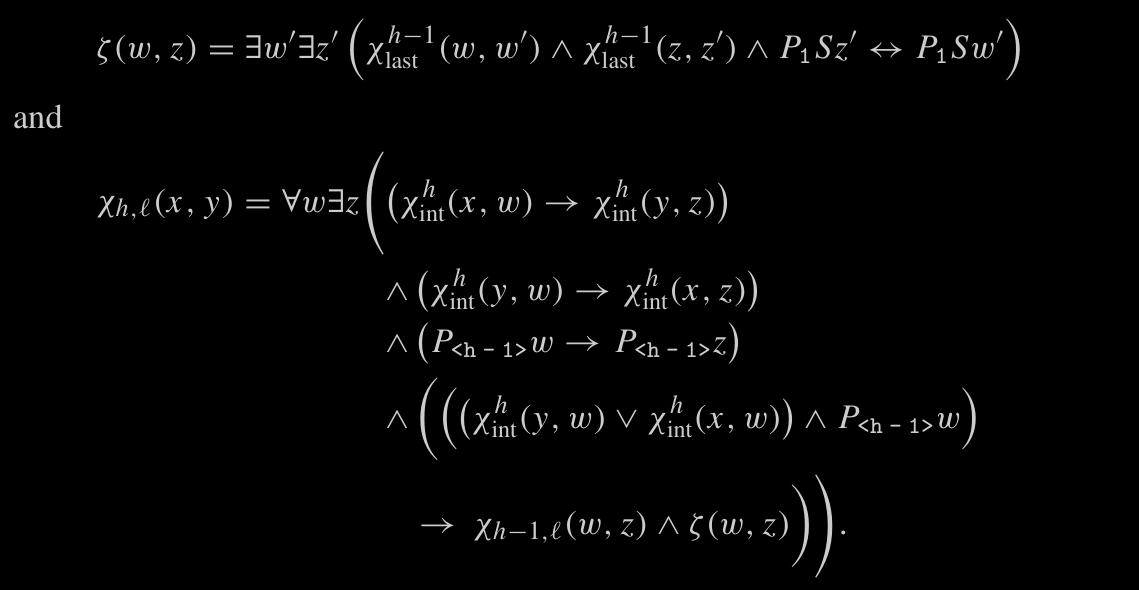
note:

• show that it is of complexity $O(h+l)$
  • explain why the above statement is a lie $O(h\cdot \lg h+l)$ is the actual complexity
  • Show that we can also compute it in time linear to that.
• And that we can compare number of 2^2^…^2^l (height h)

---

Efficient Encoding for $\mathbf{CNF}$ formulas and assignments

note:

• Write CNF definition on board
  • and of clauses

—

Literals

$${\mu }_h({\lambda }_i)=\{\begin{array}{ll}<\text{lit}>{\mu }_h(i)+</\text{lit}>& {\lambda }_i=X_i\\ <\text{lit}>{\mu }_h(i)-</\text{lit}>& {\lambda }_i=\neg X_i\end{array}$$

This logical formula checks if a literal starting at position $x$ evaluates to $\top$:

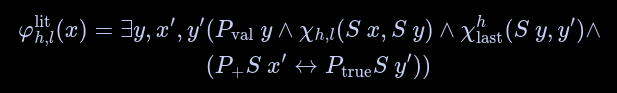
note: mention alphabets added.

—

Clause

$$\begin{array}{rl}{\mu }_h(\Delta )=⟨\text{clause}⟩& \\ & {\mu }_h({\lambda }_1)\\ & ⋮\\ & {\mu }_h({\lambda }_m)\\ ⟨/\text{clause}⟩& \end{array}$$

This formula checks if a clause evaluates to true, i.e at least one literate in the clause that evaluates to $\top$:

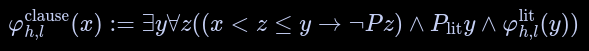
note: mention alphabets added.

—

CNF Formula

$$\begin{array}{rl}{\mu }_h(\gamma )=⟨\text{cnf}⟩& \\ & {\mu }_h({\Delta }_1)\\ & ⋮\\ & {\mu }_h({\Delta }_m)\\ ⟨/\text{cnf}⟩& \end{array}$$

This formula checks if a clause evaluates to true, i.e at least one literate in the clause that evaluates to $\top$:

note: mention alphabets added.

—

Assignment Encoding

An assignment is a function from the of propositional variables to $\{\top ,\perp \}$. For an assignment $\alpha$ we can give the following encoding to it.

$$\begin{array}{rl}{\mu }_h(\alpha )=⟨\text{assn}⟩& \\ & <\text{val}>{\mu }_h(0)\alpha (X_0)<\text{/val}>\\ & ⋮\\ & <\text{val}>{\mu }_h(n)\alpha (X_n)<\text{/val}>\\ ⟨/\text{assn}⟩& \end{array}$$

Now, given a input of the form $(\gamma ,A):\text{CNF}(n)\times \text{Assn}(n)$ we give the following encoding. ${\mu }_h(\gamma ,A)={\mu }_h(\gamma ){\mu }_h(A)$

—