202507031507

Tags : Module Theory, Homology Theory

Left and Right Inverses of Ring Homomorphisms

---

Lemma

Let $\phi :M\to N$ be an $R$-Modules homomorphism. Then

• $\phi$ has a left-invese iff the following sequence splits

$$0⟶M\stackrel{\phi }{\to }N⟶\text{coker}\phi ⟶0$$

• $\phi$ has a right-invese iff the following sequence splits

$$0⟶\text{ker}\phi ⟶M\stackrel{\phi }{\to }N⟶0$$

For the first part, if the sequence splits, the one can get $M$ back using the projection.

If $\phi$ has a left-inverse, then we can write the following diagram: 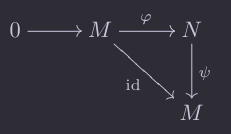We now need to show that $N$ is isomorphic to $M\oplus \text{coker }\phi$. We first get a unique morphism from $N$ to $M\oplus \text{coker }\phi$ because of the map specified in the sequence and the inverse map, due to the universal property of products.

Now we can define maps from $M\to N$, which is the inverse, and $\text{coker }\phi \to N$. For the second one, consider the inverse image of an element $a$ in the cokernel. This be the element that goes to $a$ in the cokernel and that goes to $0$ in the inverse image to $M$. The uniqueness of this comes from the universal property of Kernels and Cokernels. No using the universal property of coproducts, we get a unique map from $M\oplus \text{coker }\phi$.

The other direction seems to be the dual.

---

References

• Modules
• Split Exact Sequences
• Kernels and Cokernels
• Universal Property of Products and Coproducts
• Direct sum of Modules