202506101206

Tags : Category Theory

A Categorical notion of Equivalence Relation

---

Definition

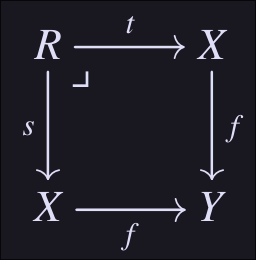
The Kernel Pair of a morphism is a pullback square along itself as given in the diagram:

We get that $(s,t):R\rightarrowtail X\times X$ is a monomorphism, so $R$ is a sub-object of $X\times X$. In the category $\text{Set}$, this corresponds to a relation on $X$, these sub-objects define an equivalence relation in the following sense.

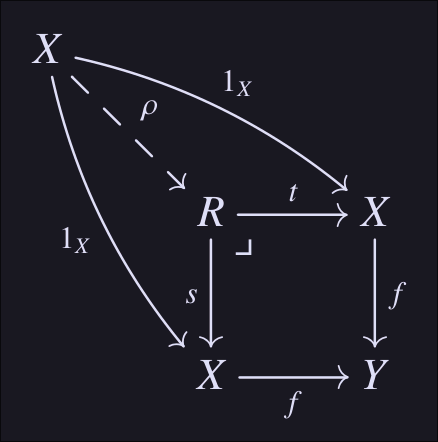
This shows that the morphism $(1_X,1_X)$ can be factorized through $(s,t)$ and can be thought of as being a part of the relation. This gives reflexivity.

Then there is the map $\sigma$:

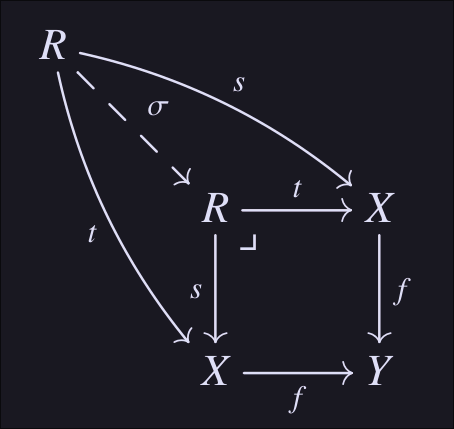
This map states that $t\sigma =s$ and $s\sigma =t$, which indicates symmetry, that is, the relation $(t,s)$ is also contained inside $(s,t)$ and vice versa.

To define Transitivity map, we first define the domain to be the pullback of $t$ and $s$ as follows: 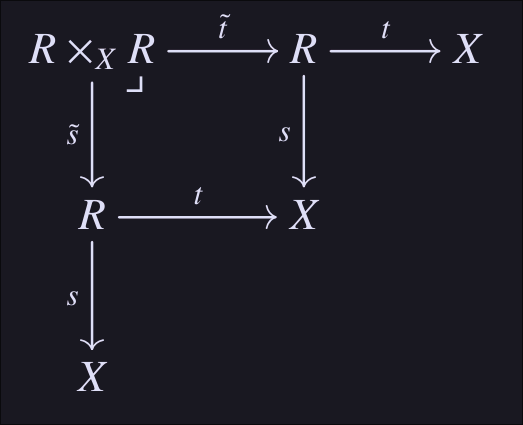These would be all pairs of elements in $R$

---

References

• Kernels and Cokernels
• Limits and Colimits
• Pullbacks and Pushouts